std::numeric_limits являється шаблонним класом, який дозволяє визначити обмеження системи відносно числових типів, на якій компілюється бібліотека. Оголошення класу приблизно виглядає наступним чином:
template <typename T>
class numeric_limits
{
public :
static const bool is_specialized = false ;
static T min() throw() ;
static T max() throw() ;
static const int digits = 0 ;
static const int digits10 = 0 ;
static const bool is_signed = false ;
static const bool is_integer = false ;
static const bool is_exact = false ;
static const int radix = 0 ;
static T epsilon() throw() ;
static T round_error() throw() ;
static const int min_exponent = 0 ;
static const int min_exponent10 = 0 ;
static const int max_exponent = 0 ;
static const int max_exponent10 = 0 ;
static const bool has_infinity = false ;
static const bool has_quiet_NaN = false ;
static const bool has_signaling_NaN = false ;
static const float_denorm_style has_denorm = denorm_absent ;
static const bool has_denorm_loss = false ;
static T infinity() throw() ;
static T quiet_NaN() throw() ;
static T signaling_NaN() throw() ;
static T denorm_min() throw() ;
static const bool is_iec559 = false ;
static const bool is_modulo = false ;
static const bool is_bounded = false ;
static const bool traps = false ;
static const bool tinyness_before = false ;
static const float_round_style round_style = round_toward_zero ;
} ;
Даний шаблонний клас має специфікації для кожного вбудованого числового типу. Даний клас не повинен бути спеціалізованим для будь-якого іншого типу.
Щоб використовувати клас необхідно підключити файл limits наступним чином:
#include <limits> /* numeric_limits */
Опис полів і методів
static const bool is_specialized = false ;
Повертає значення true для усіх числових типів, для яких був створений спеціалізований клас.
static T min() throw() ;
Кінечне мінімальше значення типу.
static T max() throw() ;
Кінечне максимальне значення типу.
static const int digits = 0 ;
Для цілих типів - кількість бітів, які число без знакового біту. Для дійсних чисел - кількість знаків мантиси.
static const int digits10 = 0 ;
Кількість цифр, які можуть бути відображеними без змін. Еквівалент для FLT_DIG, DBL_DIG або LDBL_DIG для дійсних типів.
static const bool is_signed = false ;
Містить true, коли тип може відображати знак числа.
static const bool is_integer = false ;
Містить значення true, якщо тип є цілочисельним.
static const bool is_exact = false ;
Містить true, якщо тип використовує точне представлення.
static const int radix = 0 ;
Для цілочисельних типів - число бази обрахунку (десяткова, шістнадцяткова). Для дійсних чисел - база обрахунку експоненти (еквівалент до FLT_RADIX).
static T epsilon() throw() ;
Епсилон числового типу системи, на якій була скомпільована бібліотека. Тобто різниця між одиницею і найбільшим числом, яке більше одиниці, що тип може вмістити (еквівалент FLT_EPSILON, DBL_EPSILON або LDBL_EPSILON).
static T round_error() throw() ;
Значення найбільшої помилки округлення.
static const int min_exponent = 0 ;
Мінімальне негативне значення типу, яке при зведені radix в ступінь (min_exponent-1) генерує нормалізоване число з плаваючою мантисою. Еквівалент для FLT_MIN_EXP, DBL_MIN_EXP або LDBL_MIN_EXP.
static const int min_exponent10 = 0 ;
Мінімальне негативне значення типу, при якому число 10 зведене до степені даного числа генерує нормалізоване число з плаваючою мантисою. Еквівалент до FLT_MIN_10_EXP, DBL_MIN_10_EXP або LDBL_MIN_10_EXP для дійсних типів.
static const int max_exponent = 0 ;
Максимальне позитивне значення типу, яке при зведені radix до ступеня (max_exponent-1) генерує кінечне число з плаваючою мантисою, яке можна представити. Еквівалент для FLT_MAX_EXP, DBL_MAX_EXP або LDBL_MAX_EXP.
static const int max_exponent10 = 0 ;
Максимальне ціле значення типу, при якому 10 зведена в дане число генерує нормалізоване число з плаваючою мантисою. Еквівалент до FLT_MAX_10_EXP, DBL_MAX_10_EXP або LDBL_MAX_10_EXP для дійсних типів.
static const bool has_infinity = false ;
Містить значення true, якщо тип може представляти значення позитивної безкінечності.
static const bool has_quiet_NaN = false ;
Містить значення true, якщо тип може представити без сигнальний "Not-a-Number".
static const bool has_signaling_NaN = false ;
Містить true, якщо тип може представити сигнальний "Not-a-Number".
static const float_denorm_style has_denorm = denorm_absent ;
Містить константу, яка визначає, чи тип може мати денормовані значення (значення з змінною кількістю експонентних бітів). Значення denorm_absent означає, що платворма не підтримує ненормовані значення. Значення denorm_present означає, що платформа підтримує денормовані значення типу. Значення denorm_indetermined, якщо не вдалось визначити під час компіляції.
static const bool has_denorm_loss = false ;
Містить значення true, якщо втрата точності являється скоріш причиною втрат зв’язаних з ненормованістю значь, ніж неточного результату.
static T infinity() throw() ;
Представлення позитивного безкінечного типу, якщо присутній у системі.
static T quiet_NaN() throw() ;
Значення, яке представляє без сигнальне значення "Not-a-Number", якщо таке присутнє в системі.
static T signaling_NaN() throw() ;
Представлення сигнального значення "Not-a-Number", якщо таке присутнє у системі.
static T denorm_min() throw() ;
Мінімальне позитивне ненормоване число. Для типів, які не підтримують ненормованих значень - повернене значення еквівалентне min().
static const bool is_iec559 = false ;
Містить значення true, якщо даний тип відповідає стандарту IEC-559/IEEE-754. Якщо тип підтримує стандарт IEC-559: значення констант has_infinity, has_quiet_NaN i has_signaling_NaN встановлені у значення true, а quiet_NaN і signaling_NaN повертають позитивне значення відмінне від нуля.
static const bool is_bounded = false ;
Містить true, якщо множина усіх значень, які може представити тип, являється кінечною.
static const bool is_modulo = false ;
Містить значення true, якщо тип дозволяє додати два позитивних числа, і отримати результат, який обгортається у третє число, яке являється меншим.
static const bool traps = false ;
Містить значення true, якщо тип підтримує зупинки.
static const bool tinyness_before = false ;
Містить значення true, якщо системи визначає малі числа перед їх округленням.
static const float_round_style round_style = round_toward_zero ;
Константа містить значення, яке характеризує метод округлення чисел системою. Значення round_toward_zero - якщо система округлює в сторону нуля. Значення round_to_nearest означає округлення числа до найближчого можливого значення типу. Значення round_toward_infinity означає округлення в сторону безкінечності. Значення round_toward_neg_infinity означає округлення в сторону негативної безкінечності. Значення round_indeterminate означає невизначеність методу округлення під час компілювання.
Приклад
Розглянемо приклад простої програми, яка виводить деякі з даних обмежень системи для різних типів.
#include <limits>
#include <iostream>
using namespace std ;
int main (int argc, char** argv)
{
cout << "Числові обмеження: int; double" << endl
<< "min(): " << numeric_limits<int>::min() << "; "
<< numeric_limits<double>::min() << endl
<< "max(): " << numeric_limits<int>::max() << "; "
<< numeric_limits<double>::max() << endl
<< "digits: " << numeric_limits<int>::digits << "; "
<< numeric_limits<double>::digits << endl
<< "round_error(): " << numeric_limits<int>::round_error() << "; "
<< numeric_limits<double>::round_error() << endl
<< "has_infinity: " << numeric_limits<int>::has_infinity << "; "
<< numeric_limits<double>::has_infinity << endl
<< "has_quiet_NaN: " << numeric_limits<int>::has_quiet_NaN << "; "
<< numeric_limits<double>::has_quiet_NaN << endl
<< "is_signed: " << numeric_limits<int>::is_signed << "; "
<< numeric_limits<double>::is_signed << endl
<< "min_exponent: " << numeric_limits<int>::min_exponent << "; "
<< numeric_limits<double>::min_exponent << endl
<< "max_exponent: " << numeric_limits<int>::max_exponent << "; "
<< numeric_limits<double>::max_exponent << endl
<< "radix: " << numeric_limits<int>::radix << "; "
<< numeric_limits<double>::radix << endl
<< "epsilon: " << numeric_limits<int>::epsilon << "; "
<< numeric_limits<double>::epsilon << endl
<< "is_exact: " << numeric_limits<int>::is_exact << "; "
<< numeric_limits<double>::is_exact << endl
<< "infinity(): " << numeric_limits<int>::infinity() << "; "
<< numeric_limits<double>::infinity() << endl
<< "quiet_NaN(): " << numeric_limits<int>::quiet_NaN() << "; "
<< numeric_limits<double>::quiet_NaN() << endl
<< "denorm_min(): " << numeric_limits<int>::denorm_min() << "; "
<< numeric_limits<double>::denorm_min() << endl ;
return 0 ;
}
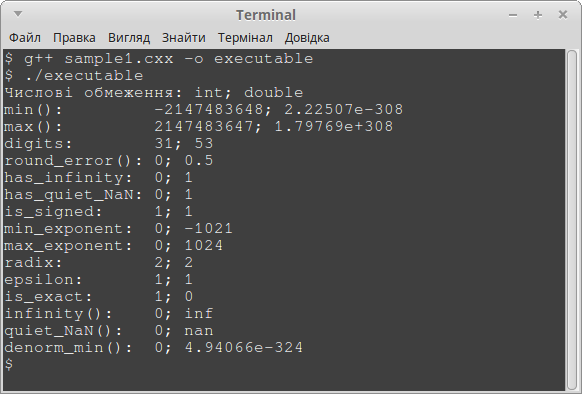
Вивід програми у термінал: